[컴파일러개론 2] 구문분석
이번주는 어휘분석에 이어 구문분석을 다룬다.
컴파일러의 전체적 구조중 전반부를 살펴보면
소스코드를 어휘분석, 구문분석, 의미 분석 를 해야한다.
어휘분석기(스캐너)을 통해 구문을 토큰으로 쪼갠 후에
구문분석기(파서)를 통해 구문분석을 진행한다.
구문 분석이란 토큰들을 트리 형식으로 만드는 것이다.
구문 분석
구문분석은 토큰을 파싱트리로 만드는 것이다.
구문 분석과 관련된 질문들은 다음의 두 가지가 있다.
1) How to describe the syntax : 프로그래밍 언어 제작자가 문법을 기술하는 방법
2) How to determine if the input token stream satisfies the syntax description : 주어진 input token stream 이 기술된 문법에 맞는지 판별하는 방법
참고) 어휘분석 때는 정규표현식으로 기술하고 상태전이도로 따라가며 판별했다.
1. How to Descrive the syntax?
CFG ( Context Free Grammer)
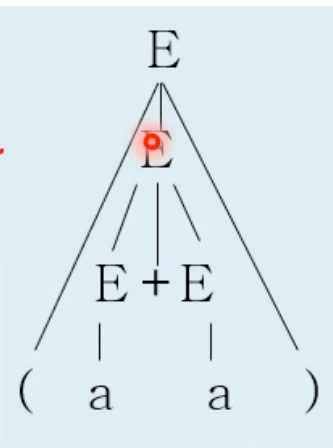
정규표현식(RE)은 토큰을 기술하는데에 좋고 DFA 로 변환하여 구현하기에도 좋다 . 하지만 Blck , expressions, statements .. 등의 Nested 구조의 구문을 표현할 때는 힘들 수도 있다. 유한한 노드로는 무한한 Nested 구조를 표현하기에 아래 그림처럼 힘들다. 따라서 그래머(CFG)를 사용한다.

CFG 는 언어의 문법을 정의하는 일반적인 방법이다. 이는 간단하고 이해하기 쉽다. 표현된 문법으로부터 자옹적으로 인식기를 구현할 수 있다.
G = (N, T, P , S) 의 네 가지 원소의 튜플로 표현한다.
N 은 non terminal 심벌 집합 , T 는 terminal 심벌 집합, P는 생성규칙 집합 S 는 시작 심벌이다.
L(G) 란 이 문버븡로 생성되는 Language 이다.
우선 Terminal 심벌 (T) 는
-a, b, c 와 같은 알파벳의 시작 부분의 소문자와 숫자 0-9
- +, - 와 같은 연산자 기호와 세미콜론, 콤마, 괄호와 같은 구분자
- 'if' 'then' 과 같이 따옴표 사이에 표기된 문법 심벌
이 Terminal 심벌이 될 수 있다.
Nontermianl 심벌 (N) 은 주어구, 관형어로 생각하면 되는데 트리로 만들기 위해서는 필수적 부분이다. 아래 요소들이 있다.
- A, B, C 와 같은 알파벳 시작 부분의 대문자로 나타내게 된다.
- S 는 보통 시작 심벌을 나타낸다.
- <stmt> 나 <expr> 과 같이 <> 로 묶어서 나타내기도 한다.
생성규칙(P)
은 예를 들어
S -> T + T
T -> '0'
T -> '1'
T -> '2'
처럼 생성 규칙과 관련된 집합이다.
만약 A->a1, A->a2 , ... , A-> ak 와 같이 왼쪽이 모두 A 라면 A-> a1|a2|...|ak| 로 간단히 표기 가능하다.
시작심벌 (S) 는 만약 아무런 언급이 없다면 첫번째 생성 규칙의 왼쪽에 있는 것이 시작 심벌이다.
CFG 의 여러 표기법으로는 BNF 와 EBNF 를 들 수 있다.
1. BNF(Backus-Naur Form)는 표준이라고 이야기하는 것인데 nonterminal 심벌은 <와 > 로 묶어서 표기하고 terminal 심벌은 문자스트링으로 표기한다.

위 첫번째 식은 정규표현식으로 l(l|d)* 와 동치이다. 그 이유로는 정규표현식에서 다음 식은
letter 다음에 letter 거나 digit 이 0번 이상 등장한다는 의미이다. 이는 CFG 에서 id 는 letter 거나 id에 letter 붙이거나 id에 digit 붙이거나 하면 다시 id 로 불릴 수 있다는 뜻이므로 처음에 letter 가 등장하고 다음에 id + letter 혹은 id + digit 이 가능하다는 의미이기 때문이다.
따라서 , S->a|Sa 는 aa*, a+ 와 동치이다.
(시작한 후 a 거나 Sa 거나 이므로 aa*, a+ (a가 한번 이상 등장함)과 동치가 된다.)
2. EBNF(Extended BNF) 는 약간 확장된 BNF 이다. 이것은 메타 심벌을 도입한 표기법이다. 반복되는 부분이나 선택적인 부분을 간결하게 표현하기 위한 특수 심벌이다.

위 예시에서 id 는 letter 로 시작하는데 letter 또는 digit 이 한번이상 반복된다는 괄호{}가 있고 07(횟수)번 반복하고 끝난다는 의미이다. 횟수도 제한할 수 있는 표기법이다.
자바로 ANTLR 문법을 사용할 때는 EBNF 를 사용한다.
( S->a|Sa 는 a+ 와 동치 S-> 엡실론|Sa 는 a*와 동치)
연습문제
1. 정규표현식을 CFG 로 바꾸어 적으시오.
- (a|b)c
- a+
- (1(0|1)*)|0
T-> 1B
T-> 0
B-> 엡실론|BA
A -> 0|1 // 1아니면 0이 터미널 심볼 / 시작심볼 T
2. How to determine if the input token stream satisfies the syntax description?
주어진 input token stream이 기술된 문법에 맞는지 판별하는 방법
문법과 언어에 대해 알아보자
문법:
s-> <주어구><동사구><주어구>-><관형구><진 주어>
언어:
"똑똑한 3학년이 모였습니다"
유도
ㅇ유도는 문법에서 언어를 생성해내는 것이다. (영작 과 비슷하다)
유도는 문법에서 문장을 생성하는 것인데 생성을 위해선 생성 규칙을 연속적으로 적용하여 Nonterminal 을 확장함으로써 얻는다.
예를 들어 이해해보자
문법 : E->E+E | E*E | (E) | a (4규칙)
언어: (a+a)
유도: E => (E) => (E+E) => (a+E) => (a+a)
위 예시에서 E+E 을 1규칙 E*E 를 2규칙 (E) 를 3규칙 a를 4규칙이라고 하자
유도 과정에서 E라는 nontermianl를 (E)로 다시쓰기를 한다.(3규칙)
그 후 (E) 를 (E+E) 로 다시쓰기를 한다.(1규칙)
그 후 E->a 인 4규칙을 사용하여 (a+E) 로 다시쓰기를 한다. (4규칙)
그 후 아직 남아있는 nonterminal 이 있어서 E->a 로 다시 다시쓰기를 한다(4규칙)
그리하여 더 이상 nonterminal 이 나오지 않아 (a+a) 라는 언어가 생성되었다.
여기서 주의할 점은 왼쪽에 있는 a 오른쪽에 있는 E
(E+E) => (a+E) 과정에서 저 E를 a 로 바꾸는 과정을 동시에 여러개를 해서는 안된다. 예를들어 (E+E) => (a+a) 처럼 넘어뛰는 것 말이다. 이렇게 넘어뛰어선 안되고
반드시 한 스텝씩 거쳐야한다.
다음은 유도 트리에 대해 알아보자
유도 트리는 유도 경로를 추상화시켜 표현한 것이다. 추상화란 눈에 보일 수 있게 한다는 의미로 해석한다면 기존의 디테일을 제거하고 보기 쉽게 만든 것이다. 유도 트리는 유도 과정에서 좌측 유도, 우측 유도를 분리하지 않는다. 좌측 유도와 우측 유도의 유도트리가 같다는 뜻이다.좌측 유도와 우측유도가 무엇일지에 대해 알아보자.
유도 과정에서 생성규칙의 '->' 다음에 하나이상의 nonterminal 심벌이 올 수 있다. 이때 유도를 좌측 유도와 유측 유도 둘 중하나를 할 수 있다.
좌측유도란 가장 좌측에 있는 nonterminal 을 먼저 대치하는 것이다
우측유도란 가장 우측에 있는 nonterminal 을 먼저 대치하는 것이다.
아래 예시로 살펴보자.

(연습문제)
1. 다음과 같은 문법이 있을 때, a*(a+a) 에 대해 좌측유도와 우측유도를 각각 하시오
문법
1. E->E+E
2. E->E*E
3. E->(E)
4. E->a
2. 각각의 경우에 대해 유도 트리를 그리시오
모호성
좌측유도와 우측유도는 유도트리가 같다. 이 둘은 항상 같을까?
사실 모든 경우에 대해 같지는 않는다. 좌측유도와 우측유도는 모호성이 없는 경우에서만 유도트리가 같다
모호성이란 문법 G에 의해 생성되는 어떤 문장이 두개 이상의 유도 트리를 갖는다면 문법 G 는 모호하다고 한다.
아래 예시를 보면 유도 트리가 다르다는 것을 알 수 있다. 다만 모호성이 있을 때는 문장이 모호한다는 표현은 쓰지 않는다. 문법이 모호한다고 한다.
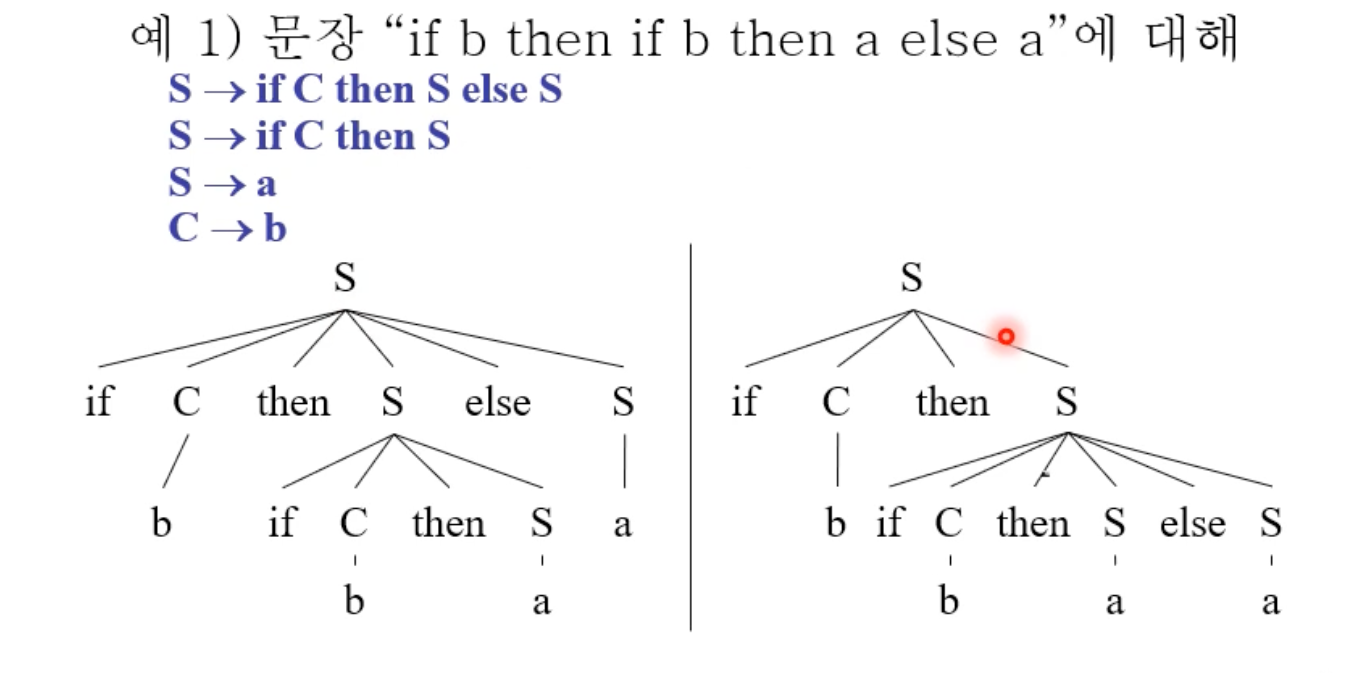
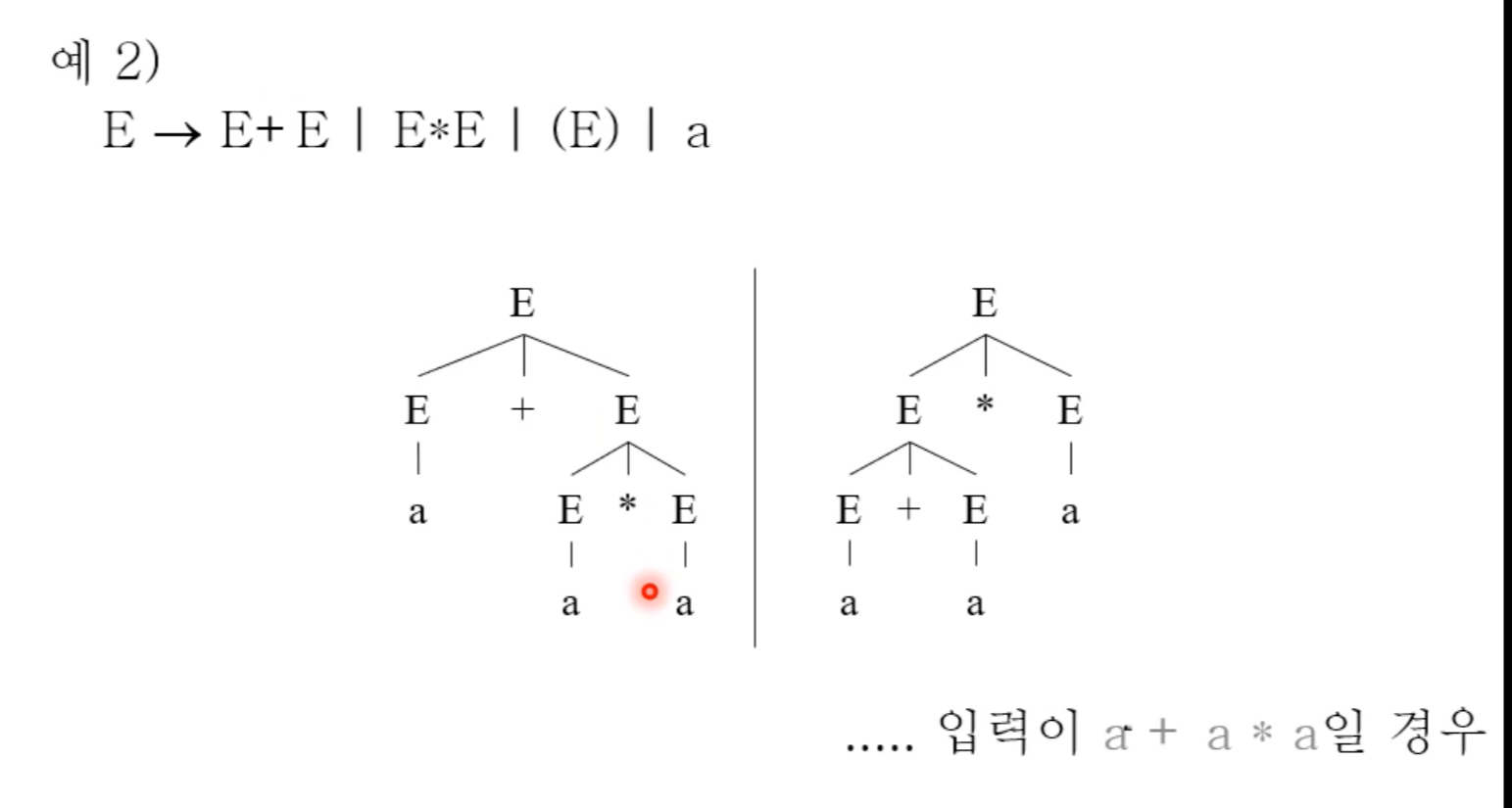
모호성을 해결하려면 어떻게 해야할까?
바로 같은 뜻을 가지는 동일한 문법을 만드는 것이다.
예를 들어 S->a 와 S->A, A->a 라는 문법은 같으므로 같은 뜻을 가지는 동일한 문법이지만 모호성이 없는 문법으로 만들어야한다.

두가지 정도의 방법이 있다.
1. 연산자 우선순위 도입 : 연산자가 여러개 있을 때 +가 먼저인지 *가 먼저인지 우선순위를 도입한다. 이를 위해 연산자마다 새로운 nonterminal 을 도입하되 recursion 을 left 나 right 둘 중하나만 두고(예를 들어 내가 나를 정의하는데 하나만 나오게 한다.E->E+E가 아닌 E-> E+T 로 정의하기), 시작심벌과 가장 가까운 쪽에 연산자 우선순위가 낮은 것을 둔다

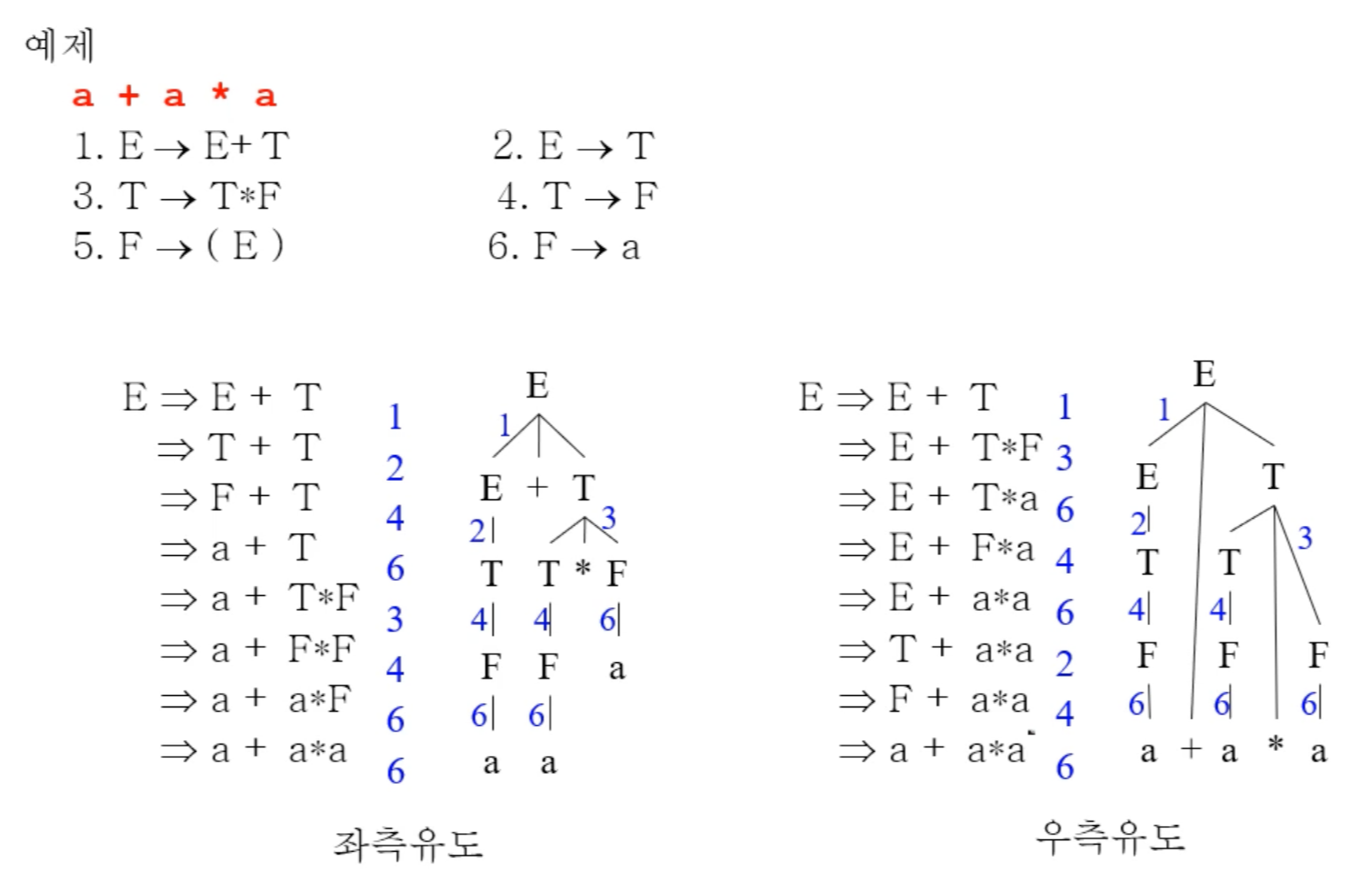
2: 결합법칙을 도입
모든 연산자는 좌측, 또는 우측결합이거나, 결합이 성립되지 않는다.
좌측결합 : a+b+c = (a+b) +c
우측결합: a^b^c = a^ (b^c)
non : a< b<c 오류(결합 불가)
원한다면 문법에서 결합법칙을 강제한다.
강제 할 땐 Recursion을 잘 배치한 후 left recursion은 좌측결합에 사용하고( A->A+a|a) Right recursion은 우측 결합에 사용한다.
(A->a^A|a)
구문분석
ㅇ구문분석은 언어에서 문법을 확인해 가는 것이다. (독해와 비슷하다)
=> 구문분석을 하려면 방법은 유도되는지 보면된다.
구문분석은 파스이다. 주어진 스트링이 정의된 문법에 의해 생성될 수 있는지의 여부(적합성)을 결정하는 과정이다.
구문분석을 위해선 유도가 되는지 보면 된다. 올바른 문장에 대해서는 '문장 구조'를 , 틀린 문장에 대해서는 오류메시지를 나타낸다.
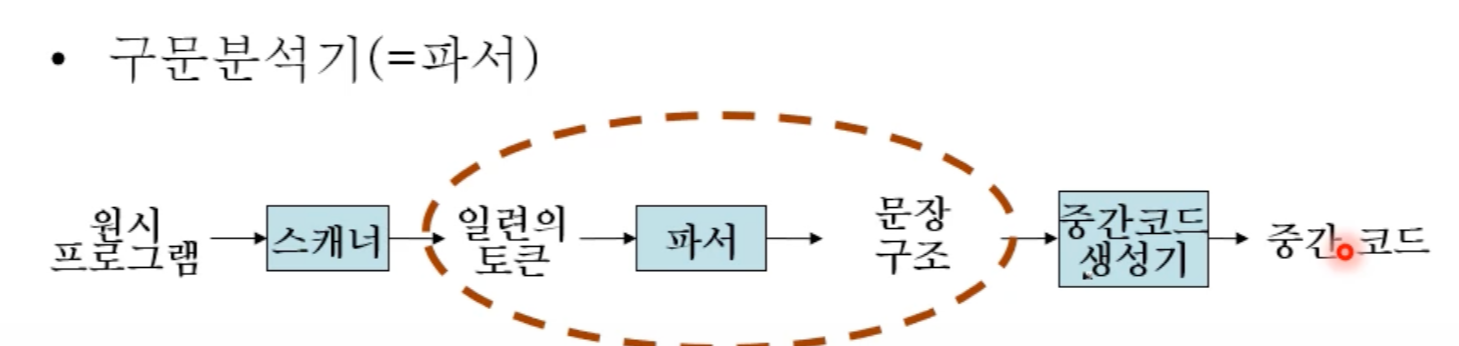
문장 구조를 나타내기 위해선 파스 트리를 사용한다. 파스 트리는 문장 구조를 나타내는 티리이며 문법을 나타내는 생성 규칙을 적용한 유도트리와 같은 모양의 트리이다.
- 루트노드 : 정의된 문법의 시작심벌
- 중간노드 : 각 생성 규칙의 좌측 nonterminal 심벌
- 단말노드 : 주어진 스트링을 생성하는 terminal tlaqjf
생성 규칙 번호 리스트는 문법의 생성규칙을 통해 유도하는 과정에서 적용되어온 일련의 생성 규칙 번호이다.
구문분석은 Top-down 방식과 Bottom-up 방식 두가지 방식이 있다. 탑다운은 루트노드로부터 시작하여 단말노드를 생성하며 확인하는 것이고, 바텀업은 단말 노드로부터 루트노드를 향하여 위로 생성하며 확인하는 것이다.
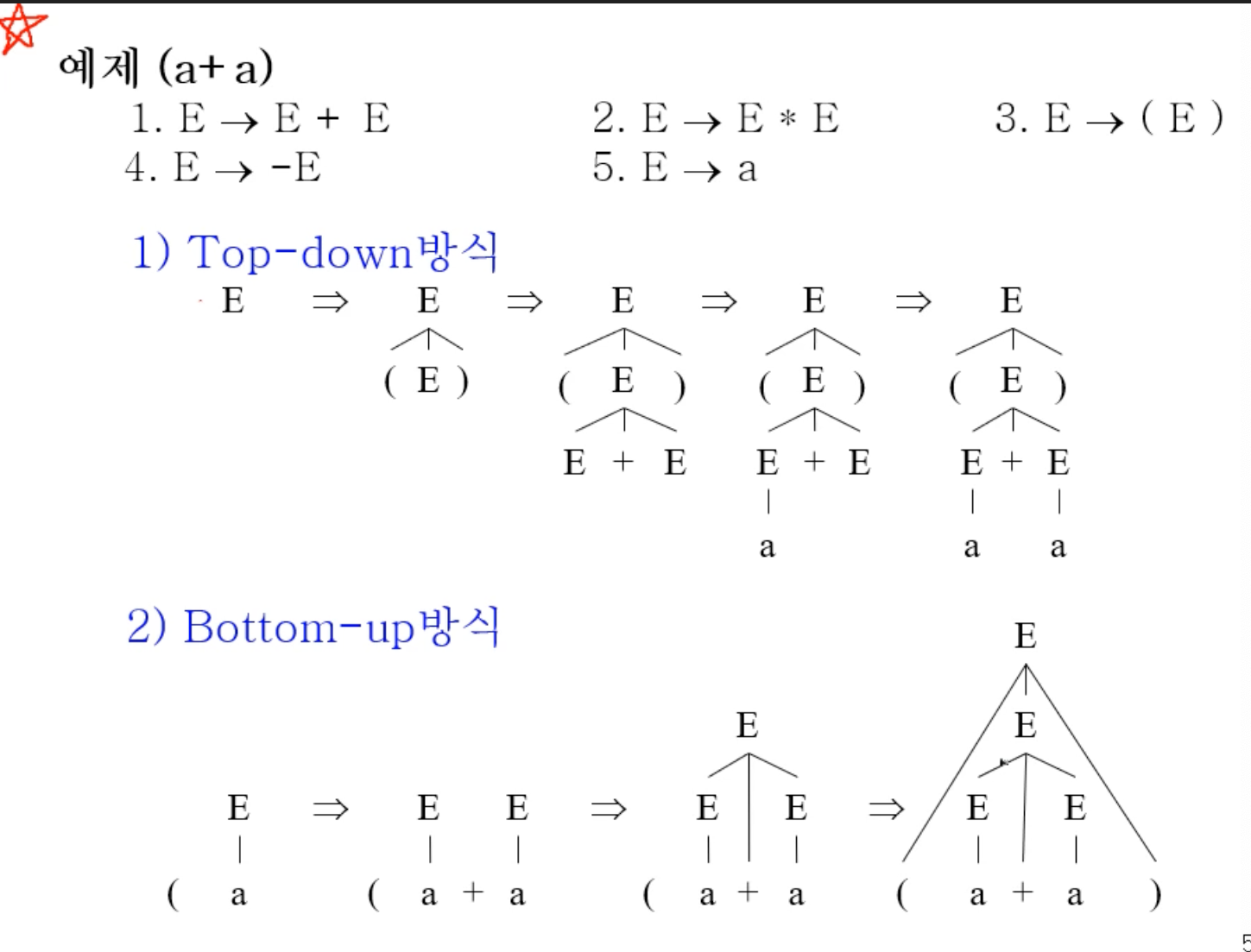
탑다운 방식은 좌측유도와 같은 순서의 생성규칙을 적용된다. "좌파스" 란 좌측유도 중 적용된 생성규칙의 리스트이다.
바텀업방식은 우측유도의 역순의 생성규칙 적용과 같다. 입력 스트링의 왼쪽에서 부터 매치한다. "우파스"란 우측유도 중 적용된 생성규칙의 역순의 리스트이다.
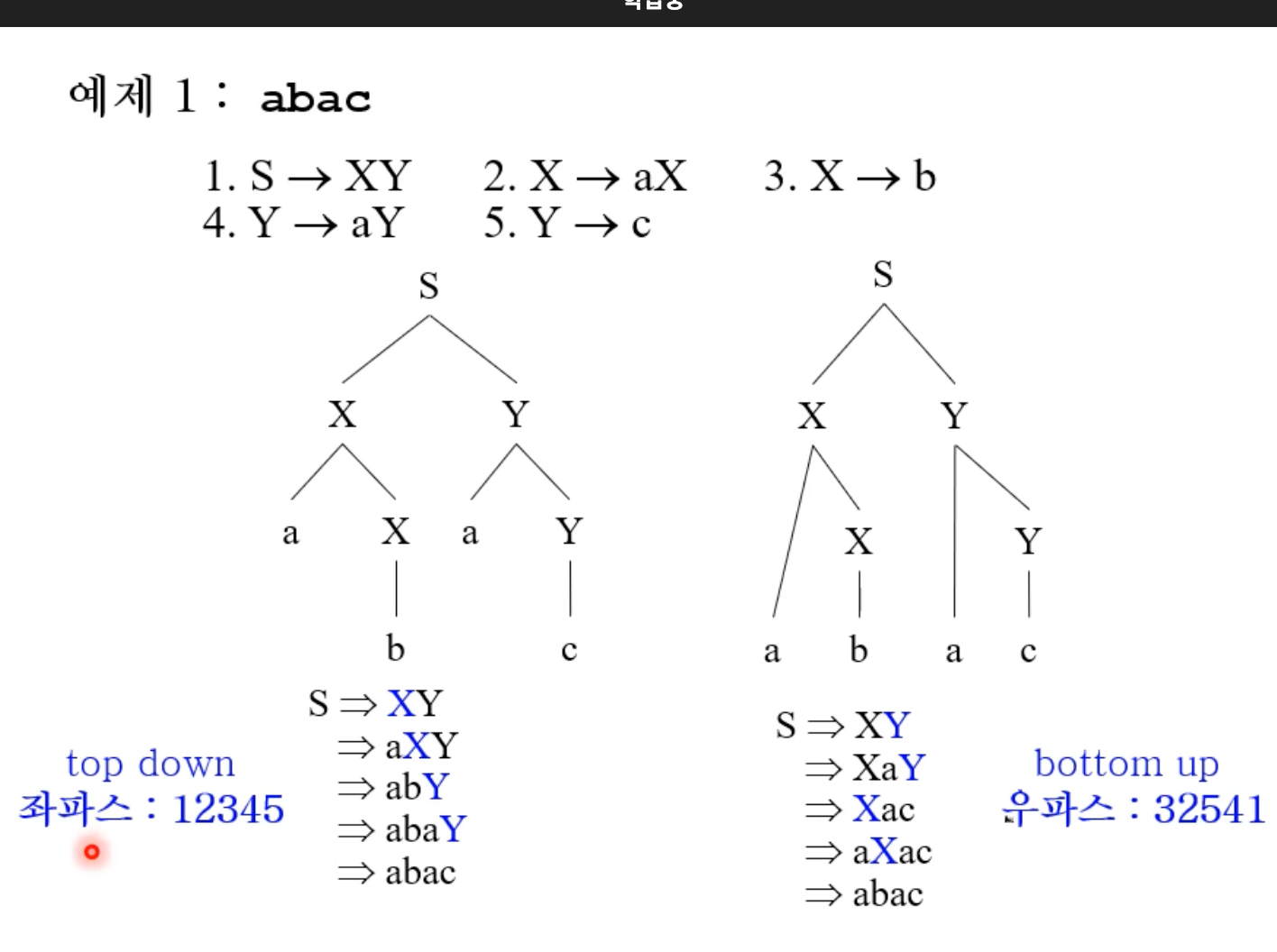
연습문제
