[선형대수 3] 행렬

 

행렬 정의

행렬이란 수 또는 변수 등의 일련의 개체들을 행(Row)과 열(Column)에 맞추어 직사각형 모양으로 순서 있게 배열하여 괄호[ ]로 묶은 것이다.

 

 

행렬 대수

행렬은 덧셈, 뺄셈, 스칼라, 곱셈 연산이 가능하다.

한 개씩 살펴보자

 

 

1. 행렬의 덧셈

아래 행렬에서 행렬 A와 B 를 더하면 같은 위치에 있는 각 원소끼리 덧셈을 진행하면 된다. 따라서 행렬의 덧셈을 하기 위해선 열의 수와 행의 수가 같아야한다.

 

 

2. 행렬의 뺄셈

아래 행렬에서 행렬 A와 B 를 빼면 같은 위치에 있는 각 원소끼리 뺄셈을 진행하면 된다. 따라서 행렬의 뺄셈을 하기 위해선 열의 수와 행의 수가 같아야한다.

 

 

 

 

3. 행렬의 스칼라 

아래 행렬에서 행렬 A에 어떤 상수 c 를 곱할 수 있다. 이때 A 에 속하는 모든 원소에 각각 c 를 곱해준다.

 

 

 

 

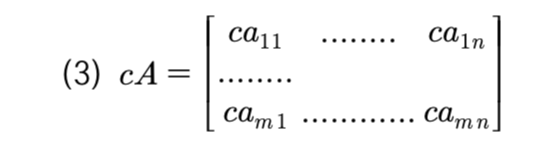
4. 행렬의 곱셈

아래 행렬에서 행렬 A와 B 를 곱하려면 다음과 같은 공식이 적용된다. 

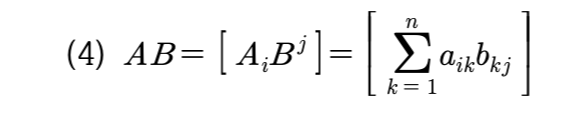
A 행렬의 i 행과 B 행렬의 j 열 원소들을 순서대로 곱한 후 다 더하면 그 수가 행렬 AB 의 (i, j) 성분이 된다.

따라서

행렬의 곱셈은 교환법칙이 성립하지 않는다. 즉 AB≠BA

 

 

 

 

 

 

대수 규칙