[기계학습 2] Bayesian Classifier

 

 

 

분류 문제를 풀 수 있는 가장 간단한 방법인 Bayesian Classifier를 먼저 살펴보자

 

분류 문제에는 

0이냐 1이냐와 같은 간단한 문제 Binary Classification

와 0~9 중 어느것이냐 와 같은 Multiple Classification

0~9중 어느것이냐(답은 여러 개)와 같은 Multi layer Classification 

가 있는데 우선 Binary 부터 살펴볼 예정이다.

 

 

 

 

Introduction

 

---

Salman-Sea Bass Problem

: 우리는 물고기를 연어인지  농어인지 분류하고 싶다.

 - Option1 : 인간의 노력

 - Option2 : 자동 시스템

 

 

 

물고기를 컨베이너 벨트에 보내고 카메라로 찍어서 정보를 넣고  라벨링을 한다. 

사람이 분류된 모델이 맞으면 맞다 틀리면 틀리다. 판단을 해준다.

 

 

그 결과 무게와 너비 인자를 통해 두 개의 카테고리로 분류하는 모델을 만들 것이다.

 

 

물고기에 대한 정보를 무게와 너비 두개의 벡터로 나타낼 것이다.

 

 

 

우리가 알고싶은 것은 확률 정보를 알고자 하는 것이다

. 

클래스 j 에 속할 확률을 P(wj|x)로 나타낼 수 있다.

 

만약 w1 일 확율이 w2 일 확률보다 크다면 데이터 x는 클래스 1에 속할 가능성이 높다.

 

 

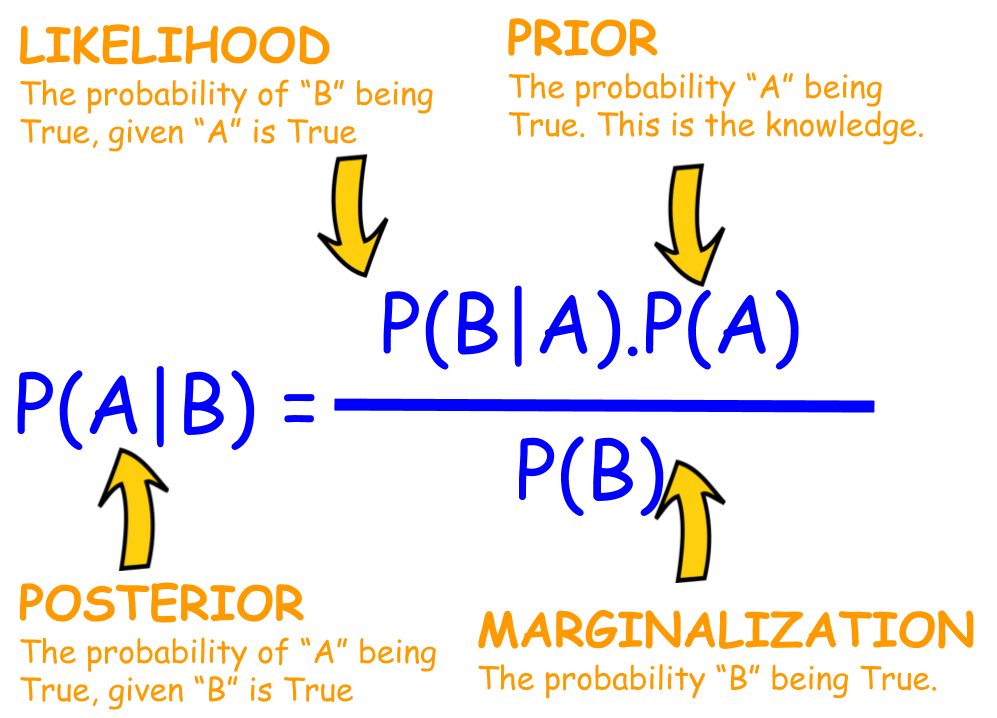
여기서 Bayes' Formula 가 활용된다.

 

Bayes' Formula 는 B에서 A 가 일어날 확률로 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리다.

 

 

Bayesian Classifier 에 적용한다면

 

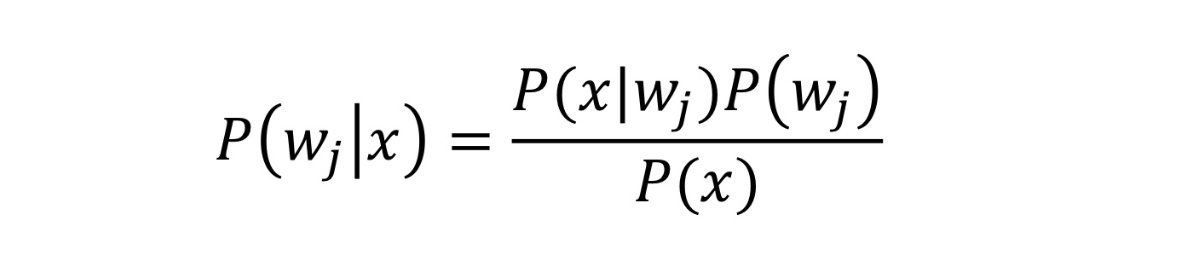
주어진 x 에 대한 클래스 j에 속하게 될 확률이 된다.

 

 

Prior

P(wj) 전체 분포 확률을 의미한다.

구하고자 하는 대상 자체에 대한 확률로

사전에 알고 있다고 가정하는 확률이다.

예를 들어 P(Salmon)는 노르웨이 바다에서 연어가 있을 확률이 된다.

 

Likelihood

Likelihood는

관찰된 데이터에 대한 확률로 class- conditional 확률이라고 불린다.

구하고자 하는 대상이 정해졌다고 가정할 때, 주어진 대상이 나올 확률이다.

예를 들어 P(x=5|Salmon) 연어 전체 중에 x 값이 5일 확률이다.

이미 존재하는 데이터를 통해 얻을 수 있는 값이다.

 

 

Posterior

계산한 값이다. classificaiton의 확률이다. prior과 likelihood에 기반하여 결정되는 값이다.

Decision = Likelihood * Prior 

 

posterior에 기반한 결정은 이 두 가지를 고려하기 때문에 사람의 결정방식과 유사하다.

지금의 observation만 고려하는 것이 아닌 이전의 observation을 고려하는 것이다.

 

 

결정할 때 Posterior 가 더 큰 쪽으로 결정하고 나머지 한쪽은 에러가 된다.

 

 

 

Parameter Estimation

---