[머신러닝 유데미] Bayesian Classification
Introduction
Bayes' Theorem
스패너 예시로 이해해보자. 우리는 공장에 있다고 가정하자. 공장에는 두 대의 기계가 있다. 두 기계는 모두 스패너를 생산한다. 스패너에는 어느 기계에서 만들었는지 확인할 수 있게 되어있다. 스패너에는 고장이 있는 불량 스패너가 생산될 수도 있다. 우리는 여기서 머신1,2에서 각각 불량이 나올 확률을 구하고 싶다.
우리는 머신1이 시간에 30개의 스패너를 생산하고 머신2가 1시간에 20개의 스패너를 생산한다는 사실을 알고 있다.
그리고 전체 생산품중에 불량품은 1%라는 사실을 알고 있으며,
그리고 우리는 불량품의 50%는 머신1에서 왔고 나머지 50%는 머신2에서 왔다는 사실을 알고 있다.
그렇다면 머신2에서 생산된 스패너가 불량품일 확률은 어떻게 될까?
여기에 베이즈 정리가 사용된다.
위에서 우리가 알고있는 정보를 우선 수학적으로 정리해보자.

P(mach1), P(mach2) : 전체 생산품에서 머신1(2) 일 확률
P(defect) : 전체 생산품에서 불량품일 확률
P(Mach1 | Defect) : 불량품중에서 머신1일 확률
구하고 싶은 것은 머신2중에서 결함이 있을 확률로 P(defect|mach2) 로 나타낼 수 있다.
그러나 이에 대한 정보는 갖고 있지 않다 .
그러므로 베이즈 정리에 의해 다른 알고있는 정보들로 해당 정보를 알아내는 것이다.
아래 공식에 대입한다면

머신2중에 불량품일 확률은 전체 중 머신2일 확률, 전체중 불량일 확률, 불량품 중 머신2일 확률 로 알아낼 수 있다.

머신러닝 알고리즘에 적용하기 위해 다음과 같은 예시로 공부해보자
그래프에서 y축은 봉급, x축은 나이이고, 녹색은 운전하해서 출근하는 사람, 빨강은 걸어서 출근하는 사람이다.

만약 새로운 데이터가 들어왔을때 다음과 같은 위치에 위치한다고 하자
이 사람은 걸어갈지 운전을 할지 기존 데이터에 기반해서 예측하고 싶다.

아까 배운 베이즈 정리에 대입해보자
왼쪽 사진은 X의 특징을 가진 데이터 포인트가 걸어서 출근할 확률. / 오른쪽은 X를 가진 데이터 포인트가 운전할 확률이다.


이 두개의 확률을 비교하여 이 사람이 걸어다닐지 운전할지를 예측하는 것이다.


우리가 그래프에서 어떤 원을 잡을 때 이 원에 속하는 사람은 비슷한 데이터셋으로 분류됨을 가정한다. 원을 어떻게 잡느냐에 따라 결과가 다를 수 있음을 의미한다.
1. P(Walks) 는 전체 점 중 빨강일 확률로 여기 예시에선 10/30이다.
2. P(X) 라는게 이해가 잘 안갈 수 있다. P(X) 는 임의의 점이 해당 원에 속할 확률, 즉 데이터집합에 새로운 점을 추가할 확률로 잡을 수 있다.
여기서는 전체 관측 점 30개 중 해당 원에 속하는 점들의 수 4개 이므로, 4/30 이다.

3. P(X|Walks) 는 걷는 사람중 X에 속할 확률로 여기서는 빨간점 중 X일 확률이다.
빨간점 10개중 원에 속하는건 3개이므로 3/10 이다.



이제 여기서 4번 Posterior Probability 을 구할 수 있다. P(Drivers|X) 도 비슷하게 구할 수 있다.
구해보면 특징 X를 가진 사람이 걸어올 확률은 0.75 운전해올 확률은 0.25이다.
이 사람은 걸어서 올 확률이 더 크므로 빨간점으로 예측될 것이다.
여기서 한 가지 궁금증이 생긴다.
이 정리는 왜 Naive 라고 불릴까?
베이즈 정리는 몇 가지 독립적인 가정을 필요로 하고, 거기에 의존하기 때문에 Naive 하다고 한다. 위 예시에서 우리는 Salary 와 Age 로 걸어서 출근하는 사람과 운전해서 출근하는 사람을 확률로 구별하는 방법을 구했다.
이때 베이즈 정리에서는 나이와 봉급이 우리가 작업하는 변수와 독립적이어야 할 것을 요구한다. 봉급은 독립적이어야하고, 나이도 독립적이어야 한다.
그러나 실제 상황에서는 일반적으로 나이가 들면 봉급이 증가한다. 아주 강한 상관관계는 아니겠지만 베이즈 정리의 가정에는 어긋나므로 실제로는 아니지만 적용하기 때문에 Naive Baysian 이라고 지칭한다. 순진한 가정이기에 순진하다고 하는것 !
Naive Baysian Classifier 실습
STEP 1 : 라이브러리 호출, 데이터셋 임포트하기
구글 코랩에 들어가서 numpy, matplotlib.pyplot, pandas 모듈을 호출한다.
데이터셋을 데이터변수에 담은 뒤 독립변수는 X 에 종속변수는 y 에 담는다.

내가 사용한 데이터셋은 이것으로, Age, Salary 와 구매 여부가 나와 있다.

STEP 2 : 데이터셋을 트레이닝셋과 테스트 셋으로 분리한 후 , Feature Scaling 진행하기
우선 sklearn의 model_selection 모듈에서 train_test_split 클래스를 호출한다.
그 후 , X_trian, X_test, y_train, y_test 에 각각 트레인 테스트를 분리하여 담는다. 테스트 사이즈는 0.25로 정한다.
우리의 데이터를 보면 나이는 0-100 사이 지만 봉급은 그보다 훨씬 높은 수치라는 것을 알 수 있다 이럴땐 feature scaing 이 필요하다. 나이가 5살 늘어난것과 봉급이 5원 늘어난 건 다르듯이..
sklearn의 preprocessing 모듈에서 StandardScaler 클래스를 임포트한다. 그 후 X_train 에 맞게 fit_transform 한 후 다시 변수에 담는다. X_test 도 잊지 않고 transform 해준다.
STEP3 : 모델을 훈련시키고 confusion matrix 을 생성한다.
sklearn 에서 naive_bayes 모듈에서 GaussianNB 를 호출한다.
model 에 GaussianNB 객체를 넣은 뒤 이 모델을 훈련시킨다. X_train 과 y_train 으로 모델을 훈련시킨다.
그 후 sklearn의 metrics 에서 confusion_matrix 와 accuracy_score 을 호출한다.
y_pred 에는 X_test 에 대한 예측 결과를 넣는다. (model.predict(X_test))
그 후 컨퓨전매트릭스 객체를 생성한다. 인자로는 예측값과 실제값을 넣으면 된다.
매트릭스를 출력한뒤, 정확도도 출력해본다.
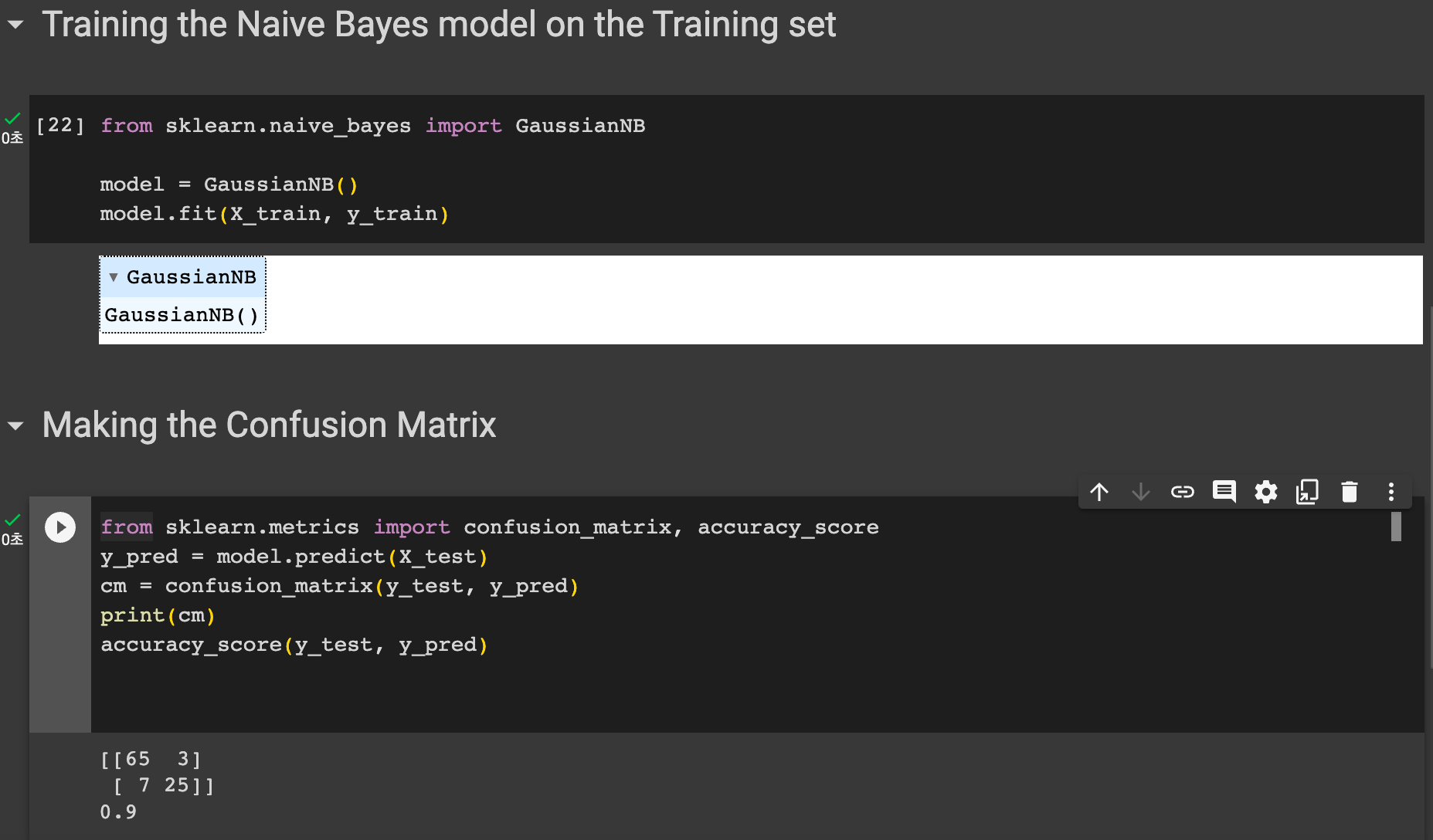
정확도는 0.9 인것을 확인할 수 있다. 아래 컨퓨전 매트릭스를 참고하면
실제로 1인데 1로 예측한것 65 / 실제론 1인데 0으로 예측함 3 / 실제로 0인데 1로 예측함 7 / 실제로 0인데 0으로 예측함 25 /
로 정확도 = 65+25 / (65+25+3+7) = 90/100 으로 0.9가 맞게 나온 것을 확인할 수 있다.
