프로그램 경진대회를 잘 하기 위한 일반적인 팁
1. 빠른 속도로 코딩
2. 문제 유형 파악
3. 알고리즘 수행 시간 및 correctness 빠른 시간 안에 파악
4. 사용하는 프로그래밍 언어에 능숙해지기 / 외부 team note 적극적 활용
5. 다양한 문제 풀며 1-4 능력 향상
6. 팀 대회일 경우 팀 구성원 별 역할 분담 확실히 하기 + 영어 지문 읽기 익숙해지기
기본 프로그래밍 기법 __숫자 처리
1. 정수 연산
프로그래밍 대회에서는 보통 int형식 사용 ( int 는 32 bit 이며 대략 범위는 -2* 10 ^9 ~ 2*10^9)
최종 결과 혹은 중간 결과가 int형의 범위를 넘어갈 거 같은 경우 long long 을 사용 가능
int a = 123456789;
long long b = a*a;
cout << b << "\n" ; /// -1757895751
*int*int = int 이므로 잘못된 값이 저장되었다.
2. 나머지 연산
- x를 m으로 나눈 나머지를 x mod m 으로 표현함
-아래 성질을 이용하면 일부 문제에서 중간 결과가 매우 커지는 것 방지 가능
-모듈로 연산에선 다음 공식이 성립한다.
(a+b) mod m = (a mod m + b mod m ) mod m
(a-b) mod m = (a mod m - b mod m ) mod m
(a*b) mod m = (a mod m * b mod m ) mod m
-ex) n!을 m으로 나눈 나머지를 구하는 코드
long long int x = 1;
for(int i=1; i <= n; i++){
x = (x*i) % m;
}
cout << x << "\n"
3. 부동 소수점 연산
-프로그래밍 경진대회에서는 환경에 따른 변수를 최소화하기 위해 보통 부동 소수점 문제는 출제가 잘 되지않음
-드물게 나오는 경우가 있으며 이 경우 '소수 몇 번째 자리까지 출력' 형식으로 주어짐
이경우 printf 함수를 이용하여 다음과 같이 나타냄
printf("%.9f\n", x); // 변수 x를 소수점 아래 9자리가지 출력
기본 프로그래밍 기법 __Recursion
1. 부분집합 생성하기
원소가 n개인 집합의 모든 부분집합을 생ㅅ어하는 일고리즘
vector<int> subset;
void search(int k) {
if (k == n+1) {
//부분 집합 처리
} else {
// k를 부분집합에 포함시킨다.
subset.push_back(k);
search(k+1);
seubset.pop_back();
//k를 부분집합에 포함하지 않는다.
search(k+1);
}
}
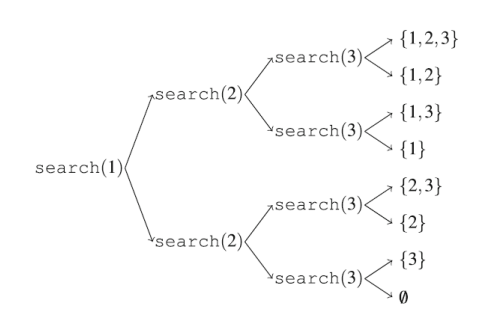
search 함수의 인자가 k일 때 이 함수는 원소 k를 부분집합에 포함할지, 아닐지를 결정한다. 그리고 두 경우에 모두 인자를 k+1 로 주고 함수를 재귀적으로 호출한다. 그러다가 k=n+1이되면 , 모든 원소를 처리했으므로 하나의 부분집합이 생성된 것이다. / 각 원소 i가 부분집합에 속하거나 속하지 않는다는 사실을 이용
recursion tree 는 다음과 같다.
1. 순열 처리하기
원소가 n개인 집합의 모든 순열을 생성하는 알고리즘,
vector<int> permutation;
bool chosen[n+1];
void search() {
if ( permutation.size() == n) {
// process permutation순열 처리
} else {
for( int i=1; i<= n; i++) {
if (chosen[i]) contunue;
chosen[i] = true;
permutation.push_back(i);
search();
chosen[i] = false;
permutation.pop_back();
}
}
}
c++ 경우 next_permutation함수 이용하여 구현 가능.
기본 프로그래밍 기법 __비트연산자
프로그램에서 n비트 자료형은 내부적으로 n비트로 이루어진 이진수로 저장된다.
비트 표현에서 맨 왼쪽은 부호를 나타내며(0: + ; 1:-) 어떤 positive number a 에 대해 -a는 2의 보수로 나타낸다. 모든 비트를 뒤집은 다음 1더함
Bitwise Operators
1. And 연산자 (x&y)
같은 위치에 1이 있는 경우에만 결과물이 1.
2. OR 연산자 (x|y)
같은 위치에 1이 하나라도 있으면 1
3. XOR 연산자 (x^y)
같은위치에 위치한 비트가 서로 다르면 1
4. NOT 연산자 (~x)
현재 비트 모두 뒤집음
Bit shift Operators
x << k : x의 비트표현에서 맨 오른쪽에 k개의 0을 추가
x >> k : 맨 오른쪽 비트 k개 제거
ex) 14(1110) << 2 -> 56(111000)
49(110001) >> 3 -> 6(110)
그 외
-x&~(1<<k) : x의 k번쨰 비트를 0으로 변환
- x^(1<<k) : x 의 k번째 비트 뒤집음
- x & (x-1) : x의 비트표현에서 가 장 오른쪽에 위치한 1을 0으로 변환
유용하게 사용할 수 있는 C++ 비트 연산자들
- __builtin_c1z(x) : x 의 맨 왼쪽부터 연속해서 존재하는 0의 개수
- __builtin_ctz(x) : x의 맨 오른쪽부터 연속해서 존재하는 0의 개수
- __builtin_popcount(x) : x 의 비트표현에서1의 개수
비트 연산자의 응용 : 집합 저장하기
C++ 에서 int형이 32비트라는 사실을 이용하여 int형 정수하나로 집합 {0.1,,,,.,31} 의 임의의 부분집합 S를 다음과 같은 int형 정수 x로 표현가능하다.
ex {1, 3, 4, 8} -> 0000 0000 0000 0000 0000 0001 0001 1010


Time Complexity
- k개의 중첩된 loop : O(n^k)
- Memoization 없이 b개의 recursive call 을 k level 에 걸쳐 수행 : O(b^k)
- k차원 table 의 각 칸을 채우는데 O(q) 시간이 걸리는 DP 문제 O(qn^k)
- 가장 빠른 comparison-based sorting 은 O(n log n) 시간이 걸린다.
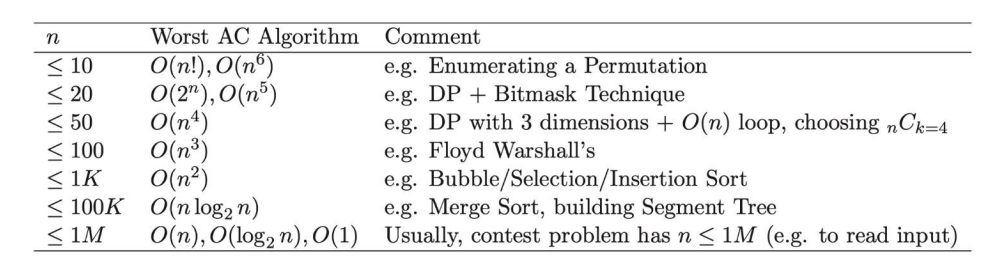
입력 시간에 따른 대략적인 시간복잡도
'알고리즘' 카테고리의 다른 글
| [알고리즘 #5] Problem Solving Paradigms(2) (0) | 2023.04.19 |
|---|---|
| [알고리즘 #4] Problem Solving Paradigms (1) (0) | 2023.04.19 |
| [알고리즘 #7] Graph Algorithm (2) (0) | 2023.04.13 |
| [알고리즘 #3] Sorting, Searching, Data Structures(2) (0) | 2023.04.11 |
| [알고리즘 #2] Sorting, Searching, Data Structures (0) | 2023.04.10 |
