Nonlinear regression
input과 output 의 관계가 꼭 선형이라고 할 수 없다. linear model 을 넘어서는 무언가가 필요해진다.
그러기 위한 가장 쉬운 방법은 선형 모델에서 다항식 모델로 넘어가는 것이다.

만약 차수가 늘어나면 담을 수 있는 파라미터가 늘어나므로 모델의 capacity가 늘어난다고 할 수 있다. 이는 반대로 일반화된 새로운 결과에 대한 성능을 잃어버릴 수도 있다.

그런데 이제 딱 맞는 차수를 찾는 건 어려운 문제이다. 그래서 충분할 정도로 차수를 높인 후 규제를 가하는 방법을 자주 쓴다.
Regularization
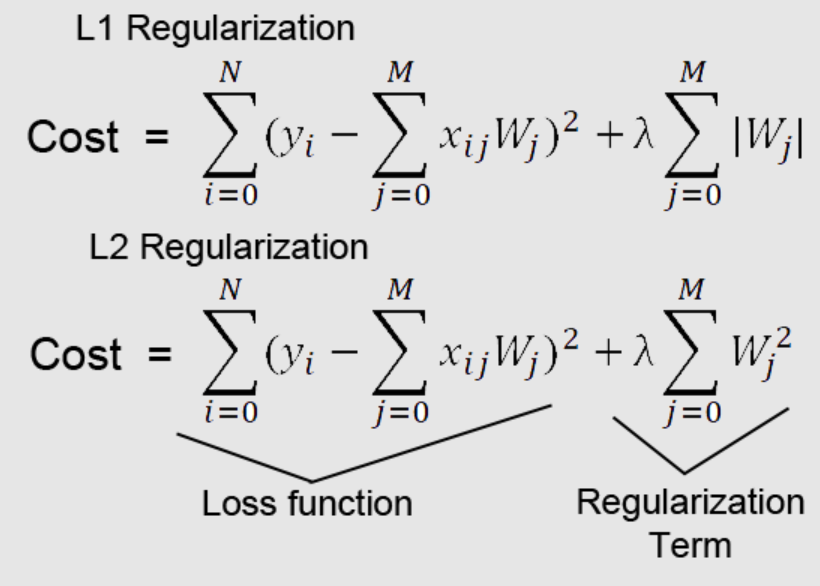
이제 nonlinear Regression 메소드들을 한 가지씩 살펴보자
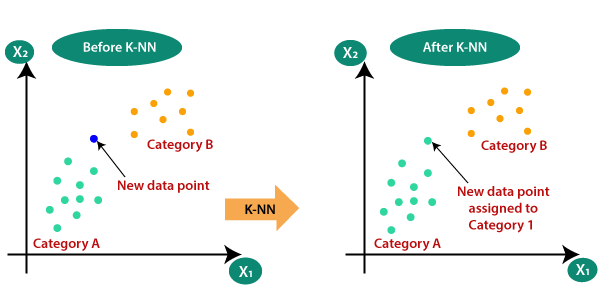
K-NN Regression
k-nearest neighbor 이라는 뜻으로 k개의 가까운 이웃을 보고 판단하는 것이다.
만약 k 가 3이라면 가장 가까운 3개를 보고 값들의 평균값으로 y값을 예측한다.

예측 규칙에는 평균을 내는 방법도 있고 가중치를 줄 수도 있다. 더 가까운 쪽에는 비중을 높이거나 하는 일 말이다.
만약 k가 작다면 가장 가까운값만 보기 때문에 그 해당값이 조금 튀는 값이라면 새로운 값도 그 편차에 영향을 받을 수 있다. 새로운 값에 대한 성능도 떨어질 수 있다.
그렇다고 만약 k 를 키운다면 근처의 너무 많은 값을 보게 되어 오히려 일반적인 경향을 따라가지 못하는 문제가 생길 수 있다. 극단적인 예시로 데이터가 30개인데 k를 30으로 한다면 전체의 평균값으로 예측하게 된다.
이 K-NN 알고리즘은 Classification 에서도 사용할 수 있다.
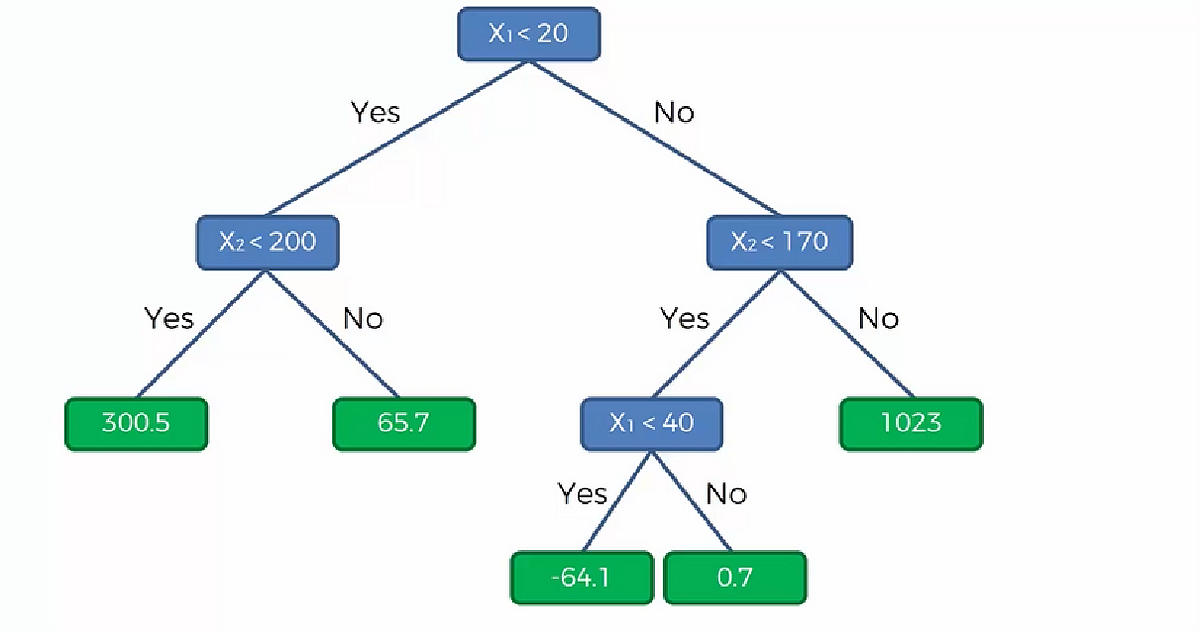
Decisoion tree regression
결정 트리라고 불리는 이 알고리즘은 몇 가지 분기를 생성하여 값을 분류하고 분류해서 데이터를 정한다.
이 알고리즘 또한 Classification 에서도 사용할 수 있다.
Nueral network regression

여러 인자들에 적당한 가중치를 곱해가며 가장 예측을 잘하는 모델을 생성한다.
hidden layer 가 많이 늘어난다면 deep neural network 이다.
Support vector regression

Support Vector Machine 은 분류(classification), 회귀(regression), 특이점 판별(outliers detection) 에 쓰이는 지도 학습 머신 러닝 방법 중 하나이다.
SVM 에는
1. SVR : Support Vector Regression
2. SVC : Support Vector Classification
두 개의 종류가 있다. 1번은 수치를 예측하는 Regression 이고 2번은 카테고리를 예측하는 Classification 이다.
SVC 은 아래 그림처럼
margin사이에 다른 데이터가 분포하고, 게다가 boundary를 넘어서 다른 집단의 데이터가 분포한다. 이러한 경우는 일반적인 데이터에 매우 많이 존재한다. 오히려 깔끔하게 boudary에 따라 분리되는 데이터를 찾는 경우가 더 힘들수도 있다.
SVM은 이러한 데이터의 경우를 생각하여, 적당한 error를 허용하며, 이러한 error를 최소화하는 boundary를 결정하는 것이다. 그리고 error를 정할 경우 모든 점들을 고려하는 것이 아니라, 선택된 점들만을 선정하여 영향을 끼칠 점과 끼치지 않을 점을 구분한다.

이와 달리 SVR은 일정 Margin의 범위를 넘어선 점들에 대한 error를 기준으로 model cost를 계산한다. 아래 그림으로 본다면 margin 바깥에 위치한 점들과 차이를 계산하는 빨간선이 곧 한 점에 있어서 error로 계산되는 것이다.

'기계학습' 카테고리의 다른 글
| [머신러닝 유데미] Decision Tree (0) | 2023.10.05 |
|---|---|
| [머신러닝 유데미] Bayesian Classification (0) | 2023.09.28 |
| [기계학습 2] Bayesian Classifier (0) | 2023.09.20 |
| [머신러닝 유데미] Classification introduction / Logistic Regression 실습 (0) | 2023.09.19 |
| [기계학습 1] Introduction / 머신러닝 정의 (0) | 2023.09.13 |
